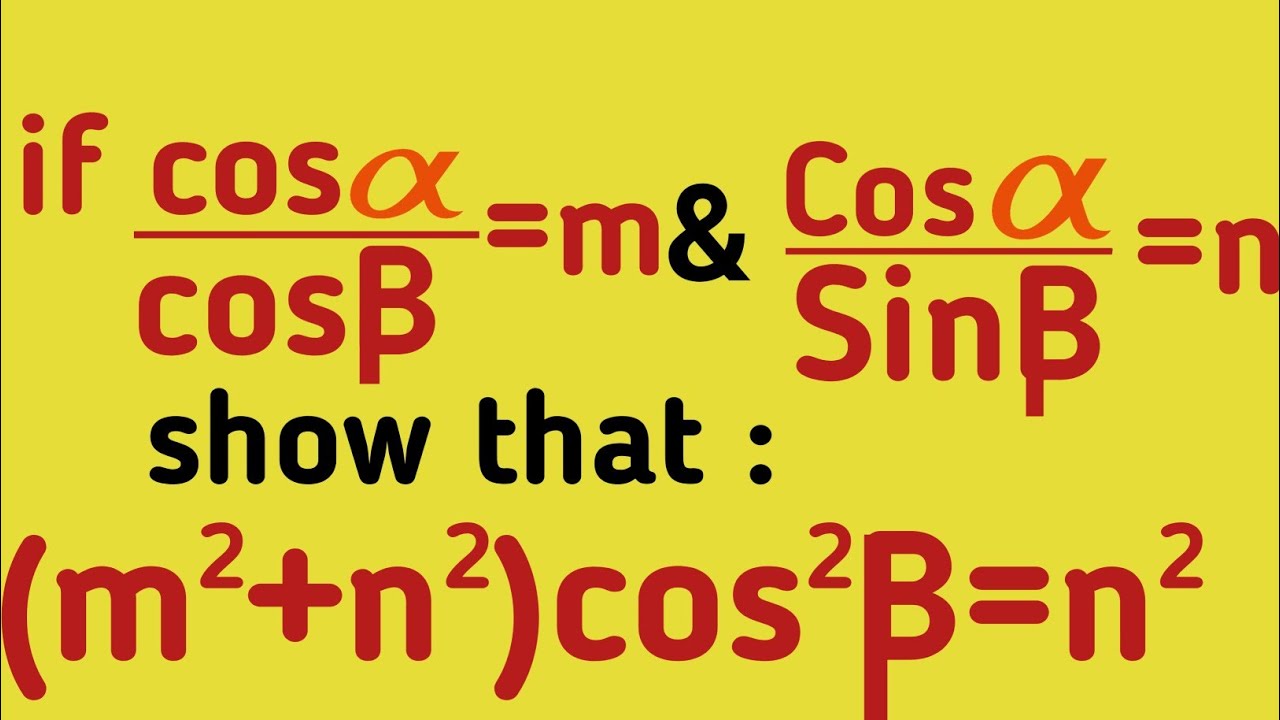Trigonometry Identity Proving is perhaps one of the most common questions incorporated in the O-Level additional math syllabus. As per the best minds associated with take my math test for me services, even the very mention of ‘Trigo proving’ will often cause even high school students to break out in cold sweats. This is primarily as, unlike most A-math theories, trigonometry proving problems do not have a standard ‘plug and play’ method of solving. Usually, most students adopt a ‘Walk one step, watch one step’ approach to solve these essential questions.
Though each question tends to be unique, there are countless ‘rule of thumb’ which students can implement not to get lost in the trigonometry multiverse. Here, we aim to highlight certain valuable techniques and strategies that will help you sail through overwhelming Trigo proving problems like an academic champion-
Express All Into Sine and Cosine
To solve all the trigo proving problems effectively, it is vital to express all sec, cosec, tan and cot in terms of sin and cos to both sides of the equation. When you do this, you are standardising both sides of the trigonometric identity, so it becomes easier to compare one side to another.
Use Pythagorean Identities To Transform Between Sin2x and Cos2x
A close look at reputed trigonometry homework help forums will enable you to understand that paying attention to adding squared trigonometry terms is crucial. Apply the Pythagorean identities whenever necessary, especially in sin2x + cos2x= 1, since all the other vital trigo terms have been converted into sine and cosine. This identity can be used to convert into and vice versa. It can also be used to remove both by turning it into 1.
Comprehend When To Apply Double Angle Formula (DAF)
Try to observe every trigonometric term in the question. Understand if there are any terms with angles 2 times another. If there are, get geared to use DAF to convert them into the same angle. For instance, if you see sin θ and cot (θ/2) in the same question, you have to use DAF since θ is 2 times (θ/2). If you still face difficulties, you can always fall back on the reputed last-minute assignment help services of the town.
Always Start From The More Complex Side
To prove a trigonometric identity, it is significant to begin from either the left-hand or the right-hand side. Apply the identities step by step until you reach the other side. However, most students are seen to start from the more complicated side. This is because it is easier to eliminate terms to make a complex function simple than to look for effective ways to introduce terms to make a simple function complex.
Remember proving trigonometry functions are an art. There are countless ways to get the answer. But, the key point to note is that whichever you take, as long as you reach the final destination, you will get the final marks.
Implement the abovementioned strategies and get ready to combat your trigonometry function problems like a warrior.
Summary
Proving trigonometric functions only becomes a piece of cake after you have conquered numerous questions and exposed yourself to all the different varieties of questions. There is no hard and fast rule to handling these complex problems since every question is a puzzle. Read this post diligently to master the art of proving trigonometry functions and nail each equation like never before.
Author Bio
Alley John is an eminent math professor at a reputed university. A proud member of MyAssignmenthelp.com for more than 12 years, he is famous for bringing smiles to the face of many students with his quality last-minute assignment help services. If you ever need assistance, feel free to contact him.